and do so very fast, over the entire brain, providing a measure of statistical significance of the results where possible.
It works in MATLAB and in Octave.
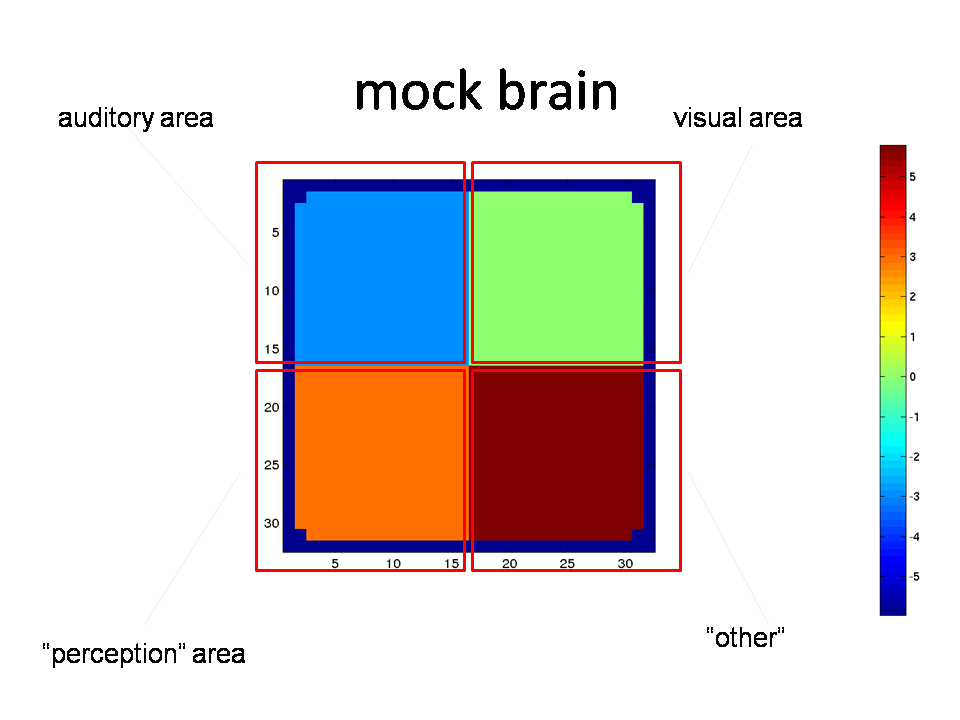
The mock brain has a single slice, divided into 4 regions-of-interest (ROIs), associated with auditory, visual and perceptual representations, as well as "other things" that are common to all conditions.
In each condition a subject will hear, see and perceive something, so each condition gives rise to a pattern of activation in each of the four ROIs.
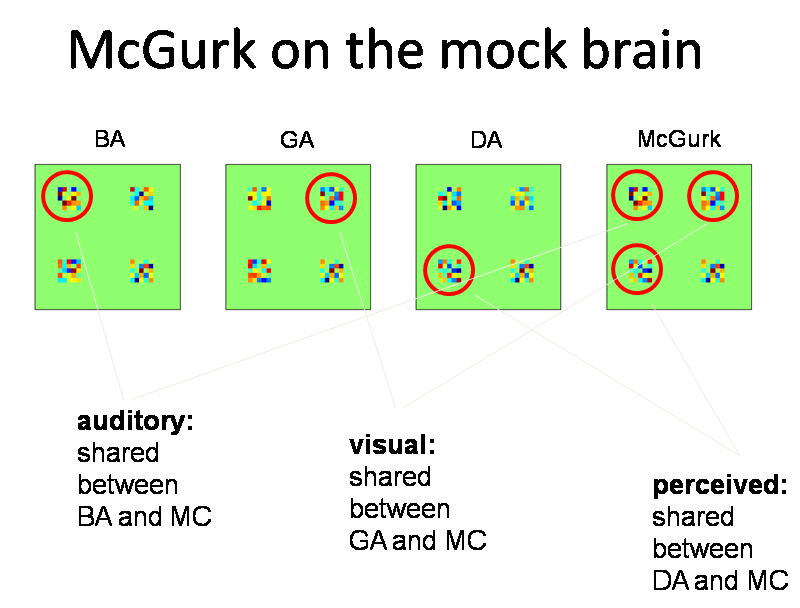
We designed the dataset so that our experimental hypothesis was true (if only life were that easy):
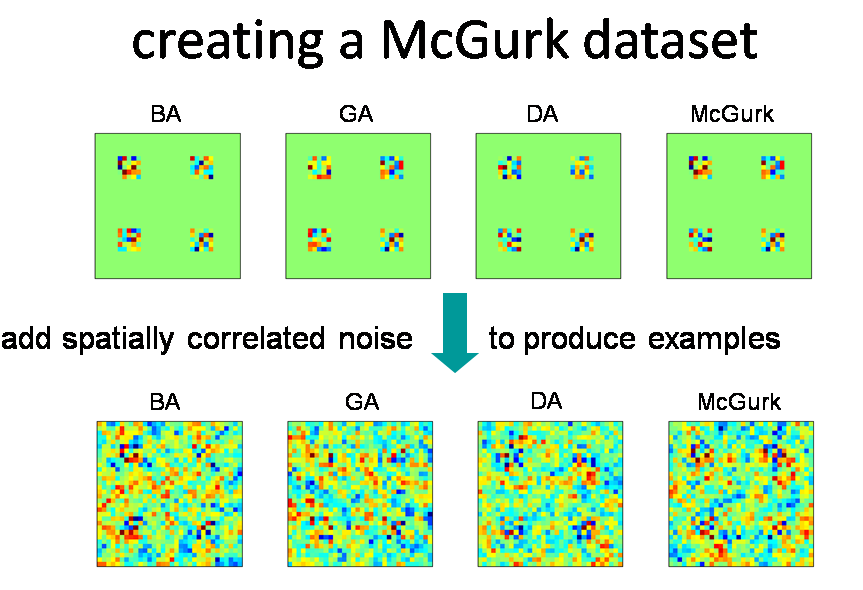
The patterns of activation in each condition were used to generate a dataset by corrupting them with noise for each trial. The dataset provided has one such image per trial, and 10 trials of each condition in each of 4 "runs". The tutorial will use this dataset and links for downloading it are provided there; for the rest of this section we will be concerned with results.
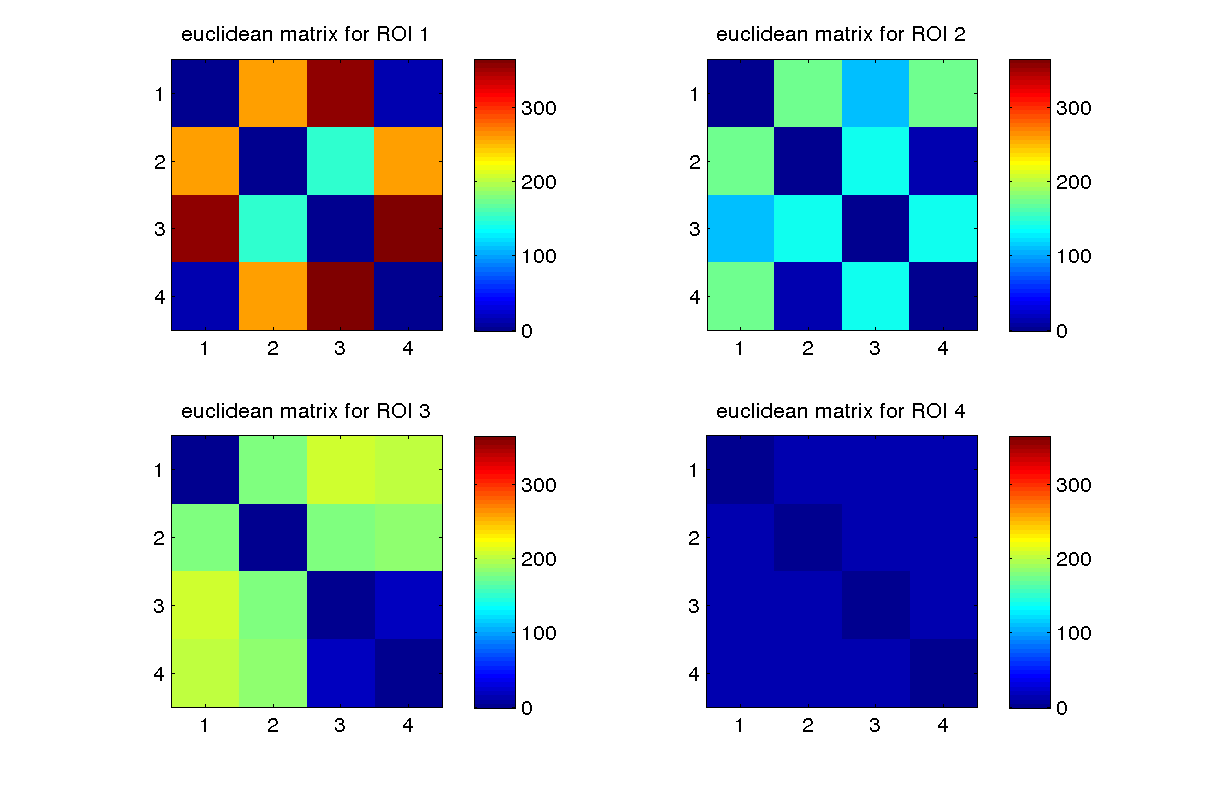
Simitar can produce a local similarity matrix between the patterns of activity in all conditions, considered over all the voxels inside a given searchlight; the measure can be correlation, euclidean distance or a number of others. If we do it for all the searchlights in the brain and plot the resulting matrices in the position of the corresponding centers, we get something like the following for correlation similarity or euclidean distances, respectively.

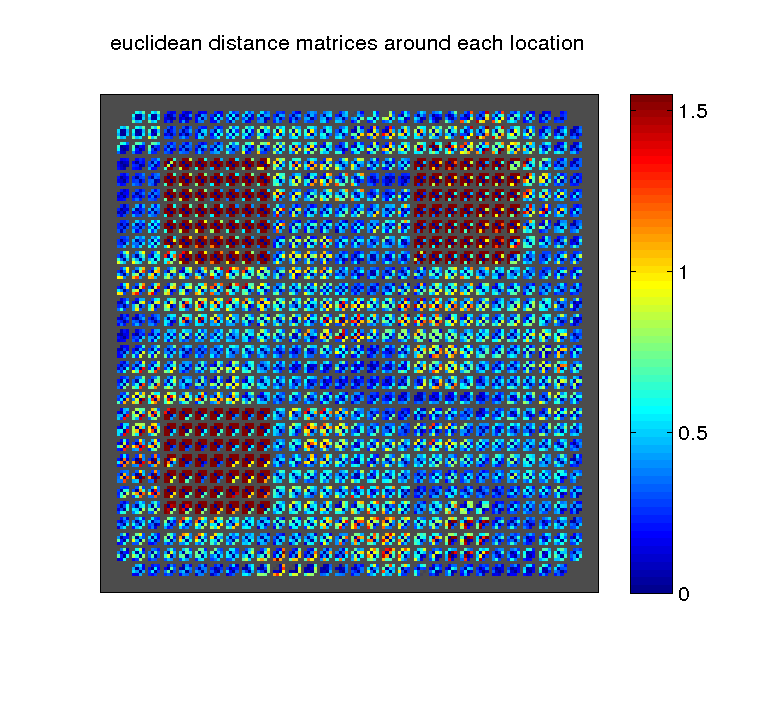
Having all local similarities can be useful if one is interested in a particular location, but in general the question is whether there are any locations where certain characteristics of similarity are present.
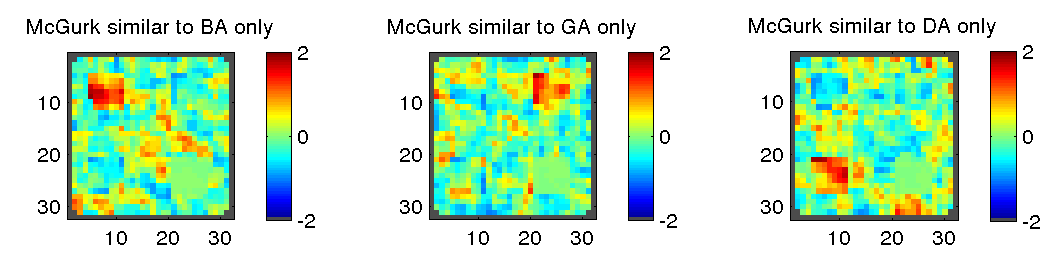
For instance, let us consider correlation matrices and suppose that we would like to find locations where BA is represented similarly to McGurk but differently from everything else. Intuitively, we want matrices where the correlation between BA and McGurk is high but that between BA and everything else (and McGurk and everything else) is low.
Simitar allows you to specify this through a similarity structure scoring scoring matrix
BA GA DA MC
BA 0 -1 -1 +1
GA -1 0 0 -1
DA -1 0 0 -1
MC +1 -1 -1 0
This matrix is multiplied elementwise by each searchlight similarity matrix and the elements of the resulting matrix are summed to produce a score. As desired, the higher the correlation between BA and McGurk the higher the score, but it will be penalized by correlation between other conditions and McGurk (0 entries are ignored). We can thus produce a similarity structure map for the similarity structure scoring matrix above (the leftmost one) as well as analogous matrices for GA and DA.
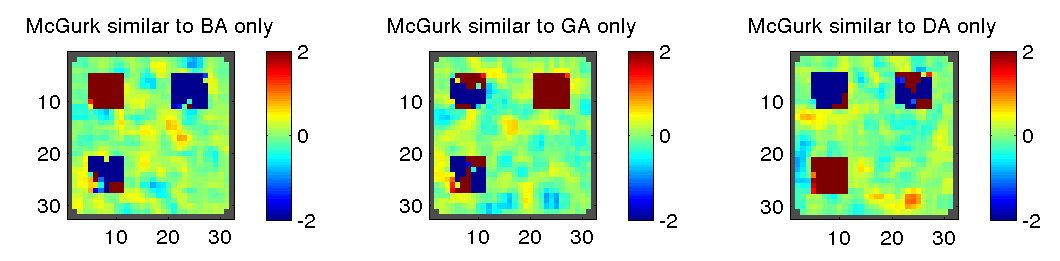
The same may be done using euclidean distance, except in this case the matrix should reward closeness between representations and penalize distance, i.e. again for BA similar to McGurk but different from everything else
BA GA DA MC
BA 0 +1 +1 -1
GA +1 0 0 +1
DA +1 0 0 +1
MC -1 +1 +1 0
which would yield the following similarity structure score maps.
The similarity structure score maps above can be used for exploratory data analysis, by looking in more detail at the locations with the highest similarity structure score. It is also possible to transform them into p-value maps by using permutation tests. Simitar supports two varieties:
These are the locations where the correlation similarity structure score was deemed significant, using 10000 permutations (of the first variety) and FDR=0.01, for similarity structure scoring matrixes picking BA similar to MC, GA similar to MC and DA similar to MC, respectively.
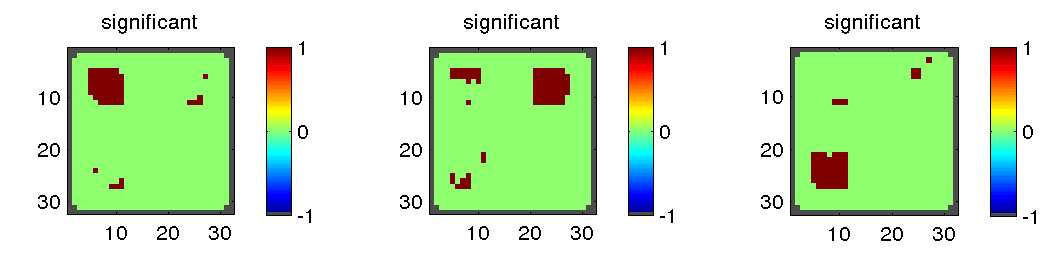


structure = [[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[-1 -1 -1 -1 -1 -1 -1 0 -1 +1 -1 -1]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[-1 -1 -1 -1 -1 -1 -1 +1 -1 0 -1 -1]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]
[ 0 0 0 0 0 0 0 -1 0 -1 0 0]];
and gives rise to these structure score maps
 for correlation
for correlation
 for euclidean distance
for euclidean distance
If we now look at the correlation matrix in the location with the highest score
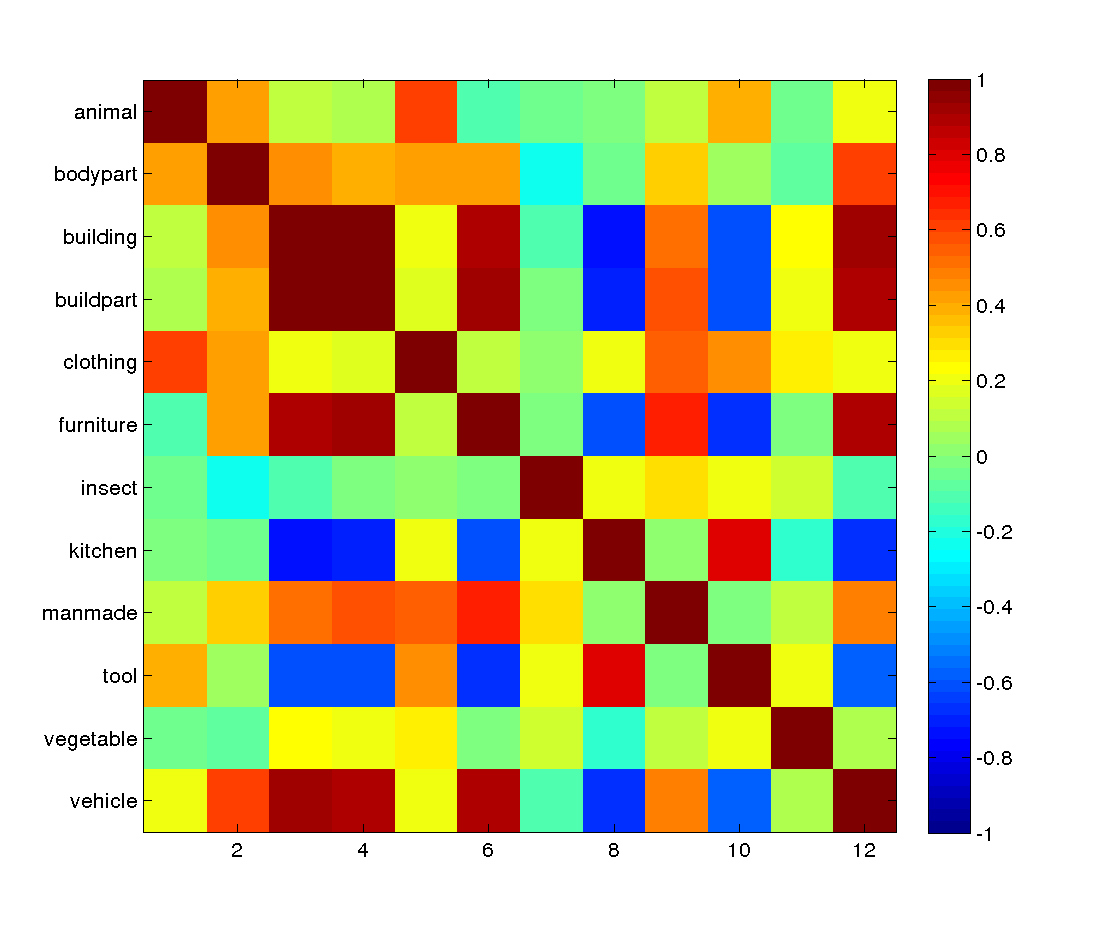
it is clear that it matches the structure we specified, in that 'kitchen utensils' and 'tools' are represented similarly to each other, but dissimilarly from other things. Note that 'buildings', 'building parts' and 'furniture' are also represented similarly to each other in the same location; the structure matrix did not reward or penalize this. In order to understand what was being represented you could now look at the patterns of activation in the appropriate searchlight (e.g. it is possible that certain conditions have similar representations because there is little activation). The tutorial shows how to find the voxels which are in the searchlight of the voxel the matrix came from, as well as their locations in 3D.
Finally, we would like to point out that the code for computing (dis)imilarity matrices across the entire brain should be fast enough that you can implement any scoring function you would like to try and do the associated permutation tests by yourself. The code for producing similarity structure score maps is simply a convenient implementation of one particular type of query -- a structure matrix -- that many users asked us for.
load('dataset_small.mat');
whos
and proceed; this might be the best thing to do the first time you go over this.
If you want to learn how to prepare data for use with Simitar, please follow the instructions given here.
You will notice that all functions take as arguments examples and labels twice. This is because the functions have been designed to operate on two entirely different sets of examples, if required, as long as they both have the same conditions present; this might occur, for instance, if you are considering data from two experiments where the conditions are the same but there is a variation in how stimuli are presented.
Internally, the computeSimilarityMap andcomputeSimilarityStructureMap functions average all examples of each condition in an example set into one example per condition. You do not have to worry about doing this yourself, and the code will work equally well if all you have is one beta image per condition. If doing permutation tests, the only difference between having many or only one example per condition is the type of test you can use (those are described above, and you can go over the tutorial without worrying about them for now). With many examples, we permute their labels prior to averaging all examples with a given label. Some functions will allow you to specify an optional groupLabels argument. This is used in conjunction with permutation tests over examples, as the labels of examples will be permuted within each group. Note that groupLabels also appears twice, again to cover the case where you have two different example sets.
measure = 'correlation';
structure = [[ 0 -1 -1 +1]
[-1 0 0 -1]
[-1 0 0 -1]
[+1 -1 -1 0]];
This will be passed to the function that creates a similarity structure score map
[structureScoreMap] = computeSimilarityStructureMap(measure,examples,labels,examples,labels,'meta',meta,'similarityStructure',structure);
Given that this is a 1 slice brain it is easy to plot the map
volume = repmat(NaN,meta.dimensions);
clf;
volume(meta.indicesIn3D) = structureScoreMap;
imagesc(volume(:,:,1)); axis square;
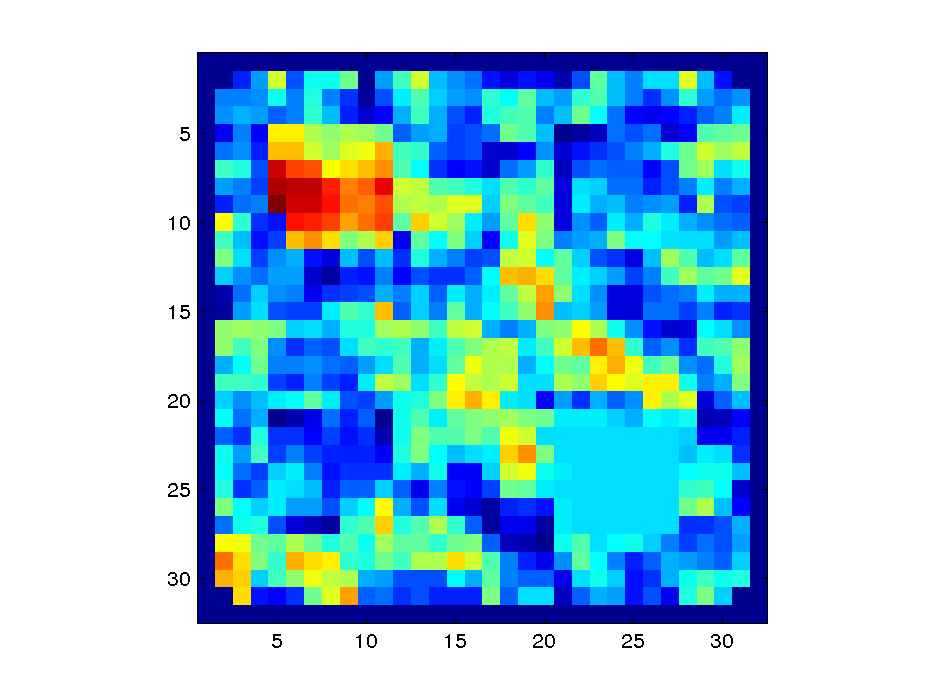
If the matrix is ternary (0, -1 and 1), the -1 and 1 present in the matrix are automatically scaled so that the same weight is given to penalization and reward, i.e. all the 1 become 1/4 in this example. You can also specify a matrix where rewards are much higher than penalizations (or vice versa), e.g. instead of 1 use 10; in that situation, the matrix will not be scaled. In our experience, a ternary matrix is a good place to start and the balancing of penalization and reward works well.
Note, also, that we specified examples and labels twice; the code can handle producing matrices involving two sets of examples, and this is just the way to specify that we only have one set. This feature might be useful if you wanted to compare the representations across two different designs involving the same conditions, say.
If you also want a map of p-values, you must also specify how many permutations to run and what kind of test to use. If you have run labels those can be used to group the examples (so that label permutations happen within-group, otherwise the code assumes that the examples belong to a single group).
testType = 'overExamples';
nPermutations = 10000;
[structureScoreMap,structurePvalueMap] = computeSimilarityStructureMap(measure,examples,labels,examples,labels,'meta',meta,'similarityStructure',structure,'permutationTest',testType,nPermutations,'groupLabels',labelsRun,labelsRun);
and you can now look at the two maps together
volume = repmat(NaN,meta.dimensions);
clf;
volume(meta.indicesIn3D) = structureScoreMap;
subplot(1,2,1); imagesc(volume(:,:,1)); axis square; title('similarity score');
volume(meta.indicesIn3D) = structurePvalueMap;
subplot(1,2,2); imagesc(volume(:,:,1)); axis square; title('score p-value');
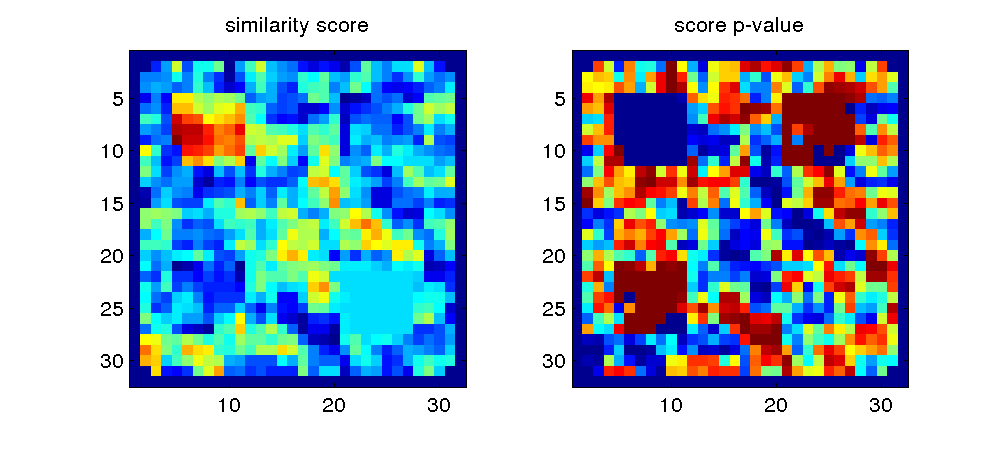
If, instead, you want to produce a map based on euclidean distance, all that needs to be changed is the measure and the scoring matrix
measure = 'euclidean';
structure = [[ 0 +1 +1 -1]
[+1 0 0 +1]
[+1 0 0 +1]
[-1 +1 +1 0]];
testType = 'overExamples';
nPermutations = 1000;
[structureScoreMap,structurePvalueMap] = computeSimilarityStructureMap(measure,examples,labels,examples,labels,'meta',meta,'similarityStructure',structure,'permutationTest',testType,nPermutations,'groupLabels',labelsRun,labelsRun);
volume = repmat(NaN,meta.dimensions);
clf;
volume(meta.indicesIn3D) = structureScoreMap;
subplot(1,2,1); imagesc(volume(:,:,1)); axis square; title('similarity score');
volume(meta.indicesIn3D) = structurePvalueMap;
subplot(1,2,2); imagesc(volume(:,:,1)); axis square; title('score p-value');

We recommend looking into similarity structure without using permutation tests, at first. You should be able to plot all slices in a single MATLAB window, and get a sense of where the similarity structure you want is present. Then you can use the approach described in the next section to look at that structure in more detail.
The tests shown above produce within-subject p-value maps. If you are interested in drawing conclusions from a group of subjects you will need to perform a second-level analysis using all the per-subject maps. For a discussion of how to do this please see the methods section of "Neural representations of events arise from temporal community structure". You can, of course, get a quick-and-dirty result by thresholding the per-subject maps and simply adding the resulting binary maps.
The similarity structure score maps are useful for getting a broad picture of where (if any) the similarity structure of interest is present at least to some degree. Once we know those locations, we can examine the corresponding similarity matrices in detail.
Let's start by computing a score map for BA similar to MC (but not others) and finding the top 10 locations
measure = 'correlation';
structure = [[ 0 -1 -1 +1]
[-1 0 0 -1]
[-1 0 0 -1]
[+1 -1 -1 0]];
[structureScoreMap] = computeSimilarityStructureMap(measure,examples,labels,examples,labels,'meta',meta,'similarityStructure',structure);
% find 10 locations where structure scores are highest
[sortedScores,sortedLocations] = sort(structureScoreMap,'descend');
top10scores = sortedScores(1:10);
top10locations = sortedLocations(1:10);
We will also need to have the matrices for all locations
measure = 'correlation';
matrixPerLocation = computeSimilarityMap(measure,examples,labels,examples,labels,'meta',meta);
size(matrixPerLocation)
(note how the size of matrixPerLocation is 4x4x#locations). Now we can pull out the matrix for each of the top 10 locations
clf;
scale = [-1 1]; % this is correlation
for t = 1:10
location = top10locations(t);
matrix = matrixPerLocation(:,:,location);
imagesc(matrix,scale); axis square;
title(sprintf('#%d highest-ranked matrix for structure',t));
pause
end
Finally, if you want to produce something like this display of all matrices in their physical locations

this code should help you get started. Note that it will do this for each slice in turn, as in most datasets that is all you may be able to fit in a single screen.
%% plot the searchlight correlation matrices in their location
%% (create a giant buffer matrix and copy correlation matrices into it)
clf;
dimx = meta.dimx; dimy = meta.dimy; dimz = meta.dimz;
scale = [-1 1];
% size of a slice in voxels
nrows = max([dimx,dimy]); ncols = nrows;
pad = 1; % plot padding between matrices
% actual size of the buffer taking into account padding
nClasses = 4;
rdim = nrows*nClasses + (nrows-1)*pad;
cdim = ncols*nClasses + (ncols-1)*pad;
buffer = repmat(NaN,rdim,cdim);
% loop over slices
for z = 1:dimz
ridx = 1;
for r = 1:nrows
rrange = ridx:(ridx+nClasses-1);
cidx = 1;
for c = 1:ncols
crange = cidx:(cidx+nClasses-1);
vidx = meta.coordToCol(r,c,z);
if vidx
% copy the matrix into the appropriate location
buffer(rrange,crange) = matrixPerLocation(:,:,vidx);
else
% not a voxel
end
cidx = cidx + nClasses + pad;
end
ridx = ridx + nClasses + pad;
end
% finally, plot the whole thing
imagesc(buffer,scale); axis square;
set(gca,'Xtick',[]); set(gca,'YTick',[]);
colorbar('vert'); title(sprintf('matrices for slice %d\n',z));
fprintf('press any key for the next slice\n'); pause;
end
nClasses = 4;
nVoxels = size(examples,2);
averageExamplePerClass = zeros(nClasses,nVoxels);
for ic = 1:nClasses
indices = find(labels == ic);
averageExamplePerClass(ic,:) = mean(examples(indices,:),1);
end
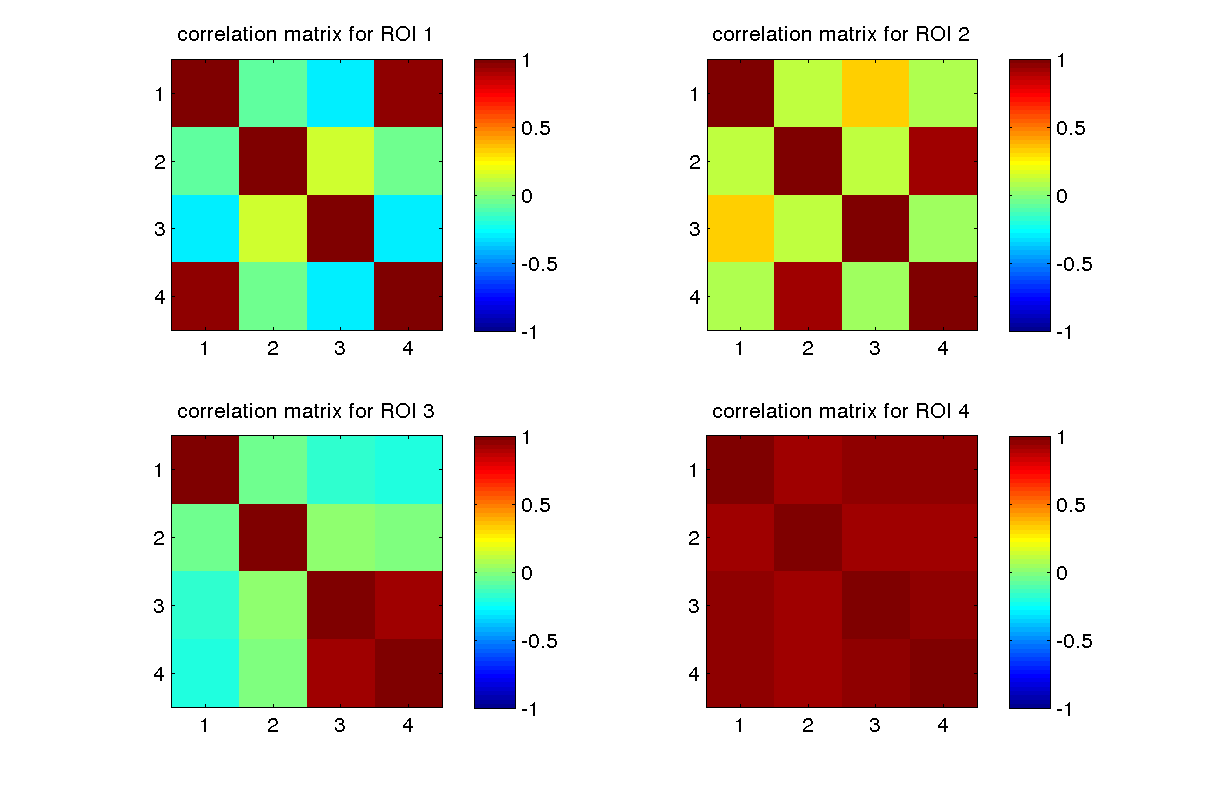
We will now compute the similarity between examples over the voxels that belong to each of the ROIs.
The meta structure included with the mock dataset has information about which columns of the examples matrix belongs to each ROI, which we will use. The tutorial on data preparation explains how to produce something like this for your dataset if you have an atlas image (instead of a brain mask where all voxels have the value 1, say).
measure = 'correlation';
nrois = length(meta.roiIDs);
for r = 1:nrois
columnsInThisROI = meta.roiColumns{r};
examplesInThisROI = averageExamplePerClass(:,columnsInThisROI);
[matrixForROI{r}] = computeExampleSimilarity(measure,examplesInThisROI,examplesInThisROI);
end
Given the matrix for each ROI, we can now produce the plot in the demo
scale = [-1 1];
clf;
nrows = ceil(sqrt(nrois)); ncols = nrows;
for r = 1:nrois
subplot(nrows,ncols,r);
imagesc(matrixForROI{r},scale); axis square; colorbar('vert');
title(sprintf('%s matrix for ROI %d',measure,r));
end

Click here to download, please.
After you unpack it, please follow the instructions in the README.txt file to install it. The tutorial should help you get started and, after that, you may want to look at the documentation in the body of each function by typing "help" and the function name from the MATLAB/Octave prompt (or reading the header of the function directly).
Thank you for giving Simitar a try! Please let us know if you encounter any bugs, have any questions or suggestions about how this documentation might be made clearer (email francisco.pereira@gmail.com).